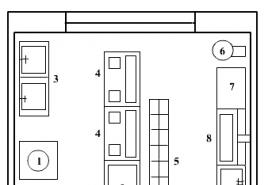
Obiecte de control dinamic de mari dimensiuni. Problemă de dimensionalitate în programarea dinamică

MINISTERUL EDUCAŢIEI ŞI ŞTIINŢEI

FEDERAȚIA RUSĂ

UNIVERSITATEA DE STAT MOSCOVA

FACULTATEA DE FIZICĂ

Departamentul de Fizică și Matematică Metode de control

SARCINI

pentru munca de curs

„Controlul optim al sistemelor dinamice liniare”

curs "Control optim"

Alcătuit de: Prof., Doctor în Științe Tehnice Afanasiev V.N.

Moscova 2014

1. SCOPUL LUCRĂRII

Proiectarea matematică a sistemelor de control liniar optim.

1. CONȚINUTUL LUCRĂRII
   1. Studierea materialului teoretic necesar din surse;
   2. Obținerea unei soluții analitice a problemei;
   3. Întocmirea unei scheme bloc a sistemului de control.
   4. Dobândirea de competențe în modelarea matematică a unui sistem de control folosind pachetul MatLab.

1. TIMP DE LUCRU

Semestrul VIII, anul IV.

Temele sunt date în a 5-a săptămână școlară.

Recepția lucrărilor finalizate se efectuează la 10 și 11 săptămâni.

PREVEDERI TEORETICE DE BAZĂ.

FORMULAREA PROBLEMEI

Multe obiecte de control pot fi descrise destul de precis prin modele dinamice liniare. Prin alegerea inteligentă a criteriilor de calitate pătratică și a constrângerilor pătratice, în acest caz se pot sintetiza dispozitive de control foarte reușite cu feedback liniar.

Fie sistemele dinamice controlate descrise prin ecuații diferențiale liniare

(1)

aici: - starea sistemului; - intrarea de control a sistemului; - ieșirea sistemului. Astfel, matricele A(t), B(t), C(t) au dimensiunile corespunzătoare: n x n, n x r, m x n. Să presupunem că nu sunt impuse restricții asupra controlului.

Să stabilim scopul sistemului din punct de vedere fizic. Fie ieșirea „dorită” a sistemului. Este necesar să găsiți un astfel de control u(t) , în care eroarea de sistem

(2)

ar fi „mic”.

De la conducere u(t) în problema luată în considerare nu este limitată, atunci pentru a evita eforturi mari în bucla de control și consumuri mari de energie, este posibil să se introducă o cerință adecvată în criteriul de calitate care să ia în considerare aceste fapte.

Este adesea important să faceți o „mică” eroare în momentul final al procesului de tranziție.

Transpunerea acestor cerințe fizice în forma uneia sau a alteia funcționale matematice depinde de multe motive. Acest capitol va lua în considerare o clasă privată de criterii de calitate având următoarea formă:

(3)

unde F, Q(t) matrici pozitive semidefinite cu dimensiune m x m ; R(t) matrice definită pozitivă cu dimensiune r x r .

Să luăm în considerare fiecare membru al funcționalului (3). Sa incepem cu. Evident, din moment ce matricea Q(t) semidefinit pozitiv, atunci acest termen este nenegativ pentru oricare e(t) și este egal cu zero la e(t)=0. Deoarece, unde q ij (t) element de matrice Q (t) și e i (t) și e j (t) componente vectoriale e(t), atunci erorile mari sunt apreciate „mai scumpe” decât cele mici.

Să luăm în considerare membrul. Deoarece R(t) este o matrice definită pozitivă, atunci acest termen este pozitiv pentru oricare și „pedepsește” mai puternic sistemul pentru acțiunile mari de control decât pentru cele mici.

In cele din urma, . Acest termen este adesea numit costul stării finale. Scopul său este de a garanta „minuțiunea” erorii în momentul final al procesului tranzitoriu.

Criteriul de calitate (3) este convenabil din punct de vedere matematic, iar minimizarea lui duce la faptul că sistemele optime se dovedesc a fi liniare.

Problema de control optim este formulată astfel: sunt date un sistem controlat dinamic liniar (1) și unul funcțional (3). Este necesar să se găsească controlul optim, adică control, sub influența căruia sistemul (1) se mișcă astfel încât să minimizeze funcționalitatea (3). Căutarea de soluții va fi efectuată pentru probleme cu o gamă deschisă de modificări ale acțiunilor de control și probleme în care acțiunile de control aparțin unui set dat.

1. EXERCIȚIU
   1. Studiați metoda de construire a controlului optim al sistemelor dinamice liniare
   2. În conformitate cu numărul de opțiune, luați starea problemei din aplicație
   3. Verificați controlabilitatea și proprietățile de observabilitate
   4. Construiește Luenberger Observer
   5. Obține o soluție analitică a problemei
   6. Desenați o diagramă bloc a unui sistem de control optim
   7. Studiați influența coeficienților de ponderare asupra calității proceselor tranzitorii și asupra valorii funcționalelor de calitate
   8. Modelarea matematică a unui sistem de control folosind pachetul MatLab

APLICARE

Obiect de control:

Functionalitate: .

Opțiunea 1

Luați în considerare când:

1. ;

Opțiunea nr. 2

Luați în considerare când:

1. ;

Opțiunea nr. 3

Luați în considerare când:

1. ;

Opțiunea nr. 4

Luați în considerare când:

1. ;

Opțiunea nr. 5

Luați în considerare când:

1. ;

Opțiunea nr. 6

Luați în considerare când:

1. ;

Opțiunea nr. 7

Luați în considerare când:

1. ;

Opțiunea nr. 8

Luați în considerare când:

1. ;

Opțiunea nr. 9

Luați în considerare când:

1. ;

Opțiunea nr. 10

Luați în considerare când:

1. ;

Opțiunea nr. 11

Luați în considerare când:

1. ;

Opțiunea nr. 12

Luați în considerare când:

1. ;

Opțiunea nr. 13

Luați în considerare când:

1. ;

Opțiunea nr. 14

Luați în considerare când:

14.1. ;

14.2. .

Opțiunea nr. 15

Luați în considerare când

15.1. ;

15.2. .

LITERATURĂ

1. Afanasyev V.N., Kolmanovsky V.B., Nosov V.R. Teoria matematică a proiectării sistemelor de control Liceu. M., 2003, 616 p.
2. Afanasiev V.N. Teoria controlului optim al sistemelor dinamice continue. Proiectare analitică. M. Facultatea de Fizică a Universității de Stat din Moscova 2011, 170 p.
3. Afanasiev V.N. Sisteme de control optime. Universitatea RUDN 2007. − 260 p.

REFERINȚE

1. Popov E.V. Sisteme expert în timp real [Resursă electronică] // Sisteme deschise - 1995. - Nr. 2. - Electron. Dan. - Mod de acces: http://www.osp.ru/text/302/178608/

2. Crossland R., Sims W.J.H., McMahon C.A. Un cadru de modelare orientat pe obiecte pentru reprezentarea incertitudinii în proiectarea variantelor timpurii. // Cercetare în Proiectare Inginerie - 2003. - Nr. 14. -P. 173-183.

3. Landmark Graphics BERBEC [Resursă electronică] - Electronic. Dan. - 2006. - Mod de acces: http://www.geographix.com/ps/vi-ewpg.aspx?navigation_id=1273

4. Schlumberger Merak [Resursa electronica] - Electronic. Dan. -2006. - Mod de acces: http://www.slb.com/content/servi-ces/software/valuerisk/index.asp

5. Gensim G2 [Resursa electronica] - Electronic. Dan. - 2006. - Mod de acces: - http://www.gensym.com/?p=what_it_is_g2

6. Thurston D.L., Liu T. Design Evaluation of Multiple Attribute Un-

der Incertitudine // Automatizarea sistemelor: cercetare și aplicații.

1991. - V. 1. - Nr. 2. - P. 93-102.

7. Paredis C.J.J., Diaz-Calderon A., Sinha R., Khosla P.K. Modele componabile pentru proiectare bazată pe simulare // Inginerie cu calculatoare. - 2001. - Nr. 17. - P. 112-128.

8. Silich M.P. Tehnologia sistemului: abordare orientată pe obiecte. - Tomsk: Vol. stat Universitatea de Sisteme de Control și Radioelectronică, 2002. - 224 p.

9. Silich M.P., Starodubtsev G.V. Model obiect pentru selectarea proiectelor de investiții pentru dezvoltarea zăcămintelor de petrol și gaze. // Automatizare, telemecanizare și comunicații în industria petrolului. - 2004. - Nr. 11. - P. 16-21.

10. Khabibulina N.Yu., Silich M.P. Caută soluții folosind un model de relații funcționale // Tehnologii informaționale

2004. - Nr. 9. - P. 27-33.

11. Algoritmul Jess Rete [Resursa electronică] - Electron. Dan. -

2006. - Mod de acces: http://www.jessru-

les.com/jess/docs/70/rete.html

UTILIZAREA CONTROALELOR DIMENSIONALE EXCESIVE PENTRU AUTONOMIZAREA IEȘIRILOR CONTROLATE ALE OBIECTELOR DE CONTROL MULTIDIMENSIONAL

A.M. Malyshenko

Universitatea Politehnică din Tomsk E-mail: [email protected]

Informațiile privind influența controalelor de exces de dimensionalitate asupra autonomizării ieșirilor obiectelor dinamice liniare staționare sunt sistematizate și sunt propuși algoritmi pentru sinteza precompensatoarelor și feedback-uri de stare și de ieșire care asigură un efect similar.

Introducere

Problema controlului autonom (independent) al componentelor ieșirii controlate a unui obiect este una dintre problemele deosebit de importante din punct de vedere practic în sinteza sistemelor de control automat (ACS), probabil pentru majoritatea obiectelor de control multidimensionale din termenii de ieșire. Se reflectă în multe publicații, inclusiv în monografii, în special în.

Problemele autonomiei pentru obiectele multidimensionale liniare staționare au fost studiate mai detaliat. Cel mai adesea se pun și se rezolvă probleme de autonomizare (decuplare) a fiecăreia dintre ieșirile unui obiect, neavând o dimensiune excesivă m a vectorului de control (CRV). Datorită imposibilității de principiu a unei astfel de soluții pentru multe obiecte de tipul specificat, această problemă este modificată într-o problemă mai generală de decuplare linie cu linie, definită ca problema Morgan, când pentru un obiect cu p ieșiri este necesar să se determine p seturi de controale t>p și legea de control corespunzătoare, cu care fiecare dintre seturi afectează doar o ieșire. Astfel, soluția este determinată în clasa sistemelor automate de control cu ​​o dimensiune excesivă a vectorului de control în ceea ce privește

comparativ cu dimensiunea vectorului variabilelor controlate.

Alături de afirmațiile de mai sus, problemele autonomizării sunt formulate și ca probleme de autonomie bloc cu bloc (decuplare), când independența este asigurată doar între coordonatele de ieșire cuprinse în diferitele lor blocuri, dar nu și în cadrul acestor blocuri (grupe), precum şi autonomie în cascadă. În acest ultim caz, dependența coordonatelor de ieșire una față de alta este de natură „în lanț” (fiecare ulterioară depinde doar de cele anterioare, dar nu și de cele ulterioare din seria stabilită pentru ele). Și în aceste cazuri, rezolvarea problemelor de autonomie necesită adesea redundanță în dimensiunea vectorului de control față de numărul de variabile controlate.

Condiţii de rezolvare a problemelor de autonomizare

Soluțiile la problemele de autonomizare se găsesc de obicei în clasa precompensatoarelor liniare sau feedback-urilor liniare statice sau dinamice, iar în aceste scopuri sunt utilizate atât aparatul matricelor de transfer (cel mai adesea), cât și metodele spațiului de stare, abordări structurale și geometrice. Ultimii doi

abordarea este completată cu succes de primele, deoarece de fapt numai cu ajutorul lor s-au putut stabili majoritatea condițiilor cunoscute de rezolvare a problemelor de autonomizare [b] și să se ofere interpretări mai profunde ale soluțiilor acestora.

Când se utilizează un precompensator pentru autonomizarea (decuplarea) ieșirilor unui obiect liniar multidimensional, adică un controler care implementează control rigid în funcția de setare ¡d(t) fără feedback, matricea sa de transfer Wy(s) este selectată din condiția

Wœ(s) = Wo(s) -W y(s), (1)

unde Wo(s) este matricea de transfer a obiectului de control și Wx(s) este matricea de transfer dorită a sistemului sintetizat, îndeplinind condițiile pentru decuplarea acestuia a ieșirilor.

Feedback-ul static liniar utilizat în aceste scopuri corespunde algoritmului de control

u(t) = F x(t) + G /u(t), (2)

si dinamic -

u (s) = F (s) x(s) + G fi(s). (3)

Feedback-urile indicate pot fi implementate atât cu transformarea regulată (matricea G este inversabilă) cât și cu transformarea neregulată a sarcinii sistemului ¡d(t).

Conform celor de mai sus, feedback-urile dinamice pot fi definite ca un caz special de extensii dinamice care completează obiectul descris de un sistem de ecuații sub forma „input-state-output” a formei

x (t) = Ax (t) + Bu (t), y (t) = C x (t),

ua (t) p_xa (t)_

unde xa(/) = ia(/), sau prin ecuația operatorului generalizat

și (5) = Г(5) x(5") + О(5) ¡л(5).

Controlul unui obiect cu un model al formei conform algoritmului (2) dă matricea finală de transfer a sistemului

F^) = C (51 - (A + B G (5))) ~1BO =

Ж0(5) . (1 - Г(5)(51 - А) -1 В)-1 О = Ж0(5) . N(5), (4)

unde Wo(s)=C(sI-AylB și #(£) sunt, respectiv, matricele de transfer ale obiectului și ale precompensatorului, echivalente în efect de feedback; I este matricea unitară de dimensiune nxn.

Transformarea canonică Morse g=(T,F,G,R,S) utilizată în abordarea geometrică cu inversabilă T,G,S a matricei de transfer Wo(s) a obiectului „Lo(C,A,B)

(A, B, C) ^ (TA + BF + R C)T,T ~lBG, SCT)

reduce Wo(s) la transformările sale bicauzale stânga și dreapta ale formei

W0(s) ^ Bi(s)-W0(s)-B2(s), (5)

unde B1(s) = S_1;

B2(s) = -G.

Din (4) și (5) rezultă că statică regulată

Feedback-urile (2) și dinamice (3) pot fi interpretate ca precompensații bicauzale, adică pot fi înlocuite cu precompensatori bicauzale echivalente ca efect. În ceea ce privește cea de-a doua, afirmația inversă este de asemenea adevărată, totuși, precompensatorul bicauzal H(s) este implementabil în conformitate cu forma unui feedback static liniar echivalent numai pentru un obiect cu Wo(s) de implementare minimă și dacă și numai dacă Wo(s) și H-1(s) - matrici polinomiale.

Din (5) putem de asemenea concluziona că precompensatorii bicauzali și feedback-ul static și dinamic regulat corespunzător nu pot modifica structura sistemului la infinit și proprietățile determinate de acesta, în special inerția (întârzierea) minimă a canalelor de control autonome. Aceste modificări pot fi realizate numai în clasa algoritmilor de control neregulat.

Condițiile de rezolvare a problemelor de autonomizare sunt asociate cu proprietățile structurale ale obiectelor controlate, descrise de listele lor de invarianți. Mai mult, setul necesar pentru aceasta este determinat de ce algoritm (compensator) este planificat să fie utilizat în aceste scopuri. În conformitate cu aceasta, pentru a determina feedback-urile dinamice de decuplare implementabile, sunt suficiente informații despre structura de intrare-ieșire a obiectului încorporat în matricea sa de transfer sau în partea minimă a descrierii din spațiul de stare. Rezolvarea acestei probleme folosind feedback-ul de stare statică este stabilită de structura internă a obiectului de control, în special pe baza studiului matricelor sale de sistem Rosenbrock sau Kronecker sau descompunerea canonică Morse.

Un precompensator rând cu rând care decuplă ieșirile obiectului poate fi determinat din (1) dacă și numai dacă m>p, iar matricele [ Wo(s) : W(s)] și Wo(s) au aceeași structură a formei Smith-McMillan la infinit.

Dacă matricea de transfer a unui obiect are rang de rând complet (o condiție necesară pentru rândul-

decuplarea, furnizată numai la t>p), apoi decuplarea poate fi asigurată de un precompensator cu matrice de transfer

unde Wnoб(s) este matricea inversă dreaptă a lui W0(s), iar k este un număr întreg care face ca Wn(s) propria sa matrice.

S-a dovedit că decuplarea utilizând feedback static obișnuit (2) este posibilă dacă și numai dacă decuplarea este posibilă folosind feedback dinamic obișnuit

(3). La rândul său, conform , acesta din urmă este posibil dacă și numai dacă structura infinită a matricei de transfer a obiectului este o unire a structurilor infinite ale rândurilor sale.

Regularitatea feedback-ului presupune de fapt că obiectul nu are redundanță în dimensiunea vectorului de control (m=p). Prin urmare, dacă decuplarea în acest caz nu este realizabilă, iar obiectul controlat are un potențial IRVU, atunci pentru a obține autonomie în controlul fiecăreia dintre cantitățile de ieșire, este indicat să profitați de această redundanță sau să faceți unele modificări de proiectare. obiectului de control pentru a obține mai întâi un IRVU de la acesta. De asemenea, trebuie avut în vedere că în situațiile în care t>p, feedback-ul regulat poate să nu conducă la rezultatul dorit, în timp ce în clasa precompensatoarelor neregulate sau același feedback se poate obține. De exemplu, pentru un obiect cu o matrice de transfer

Feedback-urile neregulate corespund precompensatorilor pur și simplu cauzali (strict proprii). Prin urmare, sistemele pe care le formează cu obiectul de control în cazul general nu vor păstra structura obiectului controlat la infinit. Acest lucru, în special, poate fi utilizat pentru a asigura stabilitatea sistemului sintetizat. Să reamintim că s-a dovedit deja că, cu ajutorul feedback-ului regulat, decuplarea și stabilitatea sistemului pot fi realizate simultan dacă și numai dacă obiectul nu are zerouri invariante instabile ale relației. Acestea din urmă sunt acele zerouri invariante £0(C,A,B) care nu sunt unu-la-unu

zerouri temporare și invariante ale subsistemelor de șiruri £;(C,A,B). Aici c, /e 1,p este /-lea rând al matricei C a obiectului. Aceste zerouri, în funcție de condițiile de decuplare, determină restricții la alegerea polilor sistemului sintetizat. În acest caz, setul de poli fix (nepermițând alocare arbitrară) a unui sistem izolat de ieșiri trebuie să includă în mod necesar toate zerourile invariante ale relației.

Astfel, algoritmul de control în cazul zerourilor invariante drepte ale relației din obiect trebuie selectat din condiția ca acesta să poată face corecția necesară în condițiile de stabilitate la proprietățile structurale ale sistemului. Aceștia, așa cum se arată mai sus, pot fi algoritmi cu feedback neregulat, care sunt implementați de fapt în clasa de sisteme cu IRVU.

O soluție completă la problema decuplării folosind feedback pentru obiectele cu zerouri invariante drepte ale relației nu a fost încă obținută. În special, pentru a-l implementa cu feedback static este necesar, după cum urmează din , să se facă structura subspațiului de controlabilitate maximă conținută în KerS suficient de bogată pentru a crește structura infinită la o listă de ordine esențiale ale obiectului. Acestea din urmă caracterizează gradul de dependență la infinit între ieșirile individuale și toate celelalte și pot fi calculate folosind formula:

pgv =ХПг -Х Пг g=1 g=1

ieșirile nu sunt decuplate folosind feedback-uri obișnuite, ci sunt decuplate de un precompensator static cu o matrice de transfer

Aici n este ordinul zero infinit al sistemului s¡ în forma Smith-McMillan a matricei de transfer a obiectului. Prima sumă din (6) este determinată pentru sistemul £0(C,A,B) ca întreg, iar a doua - pentru CS;,A,B), unde C / este matricea C fără i-a. rând. Ordinele esențiale indicate aici definesc structura minimă infinită care poate fi obținută dintr-un sistem decuplat.

Pentru feedback-ul dinamic neregulat se stabilește doar condiția de decuplare, care se rezumă la faptul că dimensiunea în exces a vectorului de control (m-p) trebuie să fie mai mare sau egală cu deficitul rangului coloanei la infinitul matricei interactorului W0( s), iar acesta din urmă trebuie să aibă rang de rând complet. Interactorul specificat al matricei de transfer a obiectului W0(s) este matricea inversă formei hermitiene W0(s). În treacăt, rețineți că ordinea a i-a esențială a unui obiect poate fi determinată prin interactorul matricei sale de transfer și este egală cu gradul polinom al coloanei a I-a.

Soluții generale pentru sinteza algoritmilor de control din clasa ACS cu IRVU, chiar și pentru obiecte liniare care oferă autonomie

rezultatele lor nu au fost încă primite. Utilizarea controalelor de exces de dimensionalitate la rezolvarea problemelor de decuplare linie cu linie (autonomia ieșirilor) a unui obiect este de fapt necesară.

aceasta conditie in acele cazuri in care obiectul controlat nu satisface conditiile de rezolvare a acestei probleme din clasa precompensatoarelor bicauzale si feedback-urile corespunzatoare acestora.

BIBLIOGRAFIE

1. Wonham M. Sisteme de control multidimensionale liniare. - M.: Nauka, 1980. - 375 p.

2. Rosenbrock H.H. Teoria multivariabilă și spațiul stărilor. - Londra: Nelson, 1970. - 257 p.

3. Meerov M.V. Cercetarea și optimizarea sistemelor de control multiconectate. - M.: Nauka, 1986. - 233 p.

4. Malyshenko A.M. Sisteme de control automat cu dimensiunea excesivă a vectorului de control. - Tomsk: Editura Politehnică Tomsk. Universitatea, 2005. - 302 p.

5. Commault C., Lafay J.F., Malabre M. Structure of linear systems. Abordări geometrice și matrice de transfer // Cybernetika. - 1991.

V. 27. - Nr. 3. - P. 170-185.

6. Descusse J., Lafay J.F., Malabre M. Solution of Morgan’s problem // IEEE Trans. Automat. Control. - 1988. - V. aC-33. -P. 732-739.

7. Morse A.S. Invarianții structurali ai sistemelor multivariabile liniare // SIAM J. Control. - 1973. - Nr. 11. - P. 446-465.

8. Aling H., Schumacher J.M. O descompunere canonică de nouă ori pentru sisteme liniare // Int. J. Control. - 1984. - V. 39. - P 779-805.

9. Hautus M.L.J., Heymann H. Linear feedback. O abordare algebrică // SIAM J. Control. - 1978. - Nr. 16. - P. 83-105.

10. Descusse J., Dion J.M. Despre structura la infinit de sisteme decuplabile liniare pătrate // IEEE Trans. Automat. Control. - 1982. -V. AC-27. - P. 971-974.

11. Falb P.L., Wolovich W. Decoupling in the design and synthesis of multi-variable systems // IEEE Trans. Automat. Control. - 1967. -V. AC-12. - P 651-669.

12. Dion J.M., Commault C. The minimal delay decoupling problem: feed-back implementation with stability // SIAM J. Control. -1988. - Nr. 26. - P. 66-88.

UDC 681.511.4

CORRECTORI ADAPTATIVI PSEUDO-LINEARI AI CARACTERISTICILOR DINAMICE ALE SISTEMELOR DE CONTROL AUTOMAT

M.V. Skorospeshkin

Universitatea Politehnică din Tomsk E-mail: [email protected]

Sunt propuși corectori adaptivi de amplitudine și fază pseudoliniari ai proprietăților dinamice ale sistemelor de control automat. A fost realizat un studiu al proprietăților sistemelor de control automat cu corectori adaptivi. Este prezentată eficacitatea utilizării corectoarelor adaptative pseudoliniare în sistemele automate de control cu ​​parametri nestaționari.

În sistemele de control automat al obiectelor ale căror proprietăți se modifică în timp, este necesar să se asigure o modificare țintită a caracteristicilor dinamice ale dispozitivului de control. În cele mai multe cazuri, acest lucru se realizează prin modificarea parametrilor controlerelor proporțional-integral-derivate (controlere PID). Astfel de abordări sunt descrise, de exemplu, în, totuși, implementarea acestor abordări este asociată fie cu identificarea, fie cu utilizarea unor metode speciale bazate pe calcule de-a lungul curbei procesului tranzitoriu. Ambele abordări necesită timp de configurare semnificativ.

Această lucrare prezintă rezultatele unui studiu al proprietăților sistemelor automate de control cu ​​un controler PID și corectori secvențiali de amplitudine și fază pseudoliniari adaptivi ai caracteristicilor dinamice. Această metodă de adaptare este caracterizată

faptul că în timpul funcționării sistemului de control, parametrii controlerului nu se modifică și corespund setărilor anterioare punerii în funcțiune a sistemului. În timpul funcționării sistemului de control, în funcție de tipul de corector utilizat, se modifică coeficientul de transmisie al corectorului sau defazajul creat de acesta. Aceste modificări apar numai în cazurile în care fluctuațiile cantității controlate apar din cauza modificărilor proprietăților obiectului de control sau din cauza impactului perturbărilor asupra obiectului de control. Și acest lucru face posibilă asigurarea stabilității sistemului și îmbunătățirea calității proceselor tranzitorii.

Alegerea corectoarelor pseudoliniare pentru implementarea unui sistem adaptiv este explicată după cum urmează. Corectorii utilizați pentru modificarea proprietăților dinamice ale sistemelor de control automate pot fi împărțiți în trei grupe: liniari, neliniari și pseudoliniari. Principalul dezavantaj al corectoarelor liniare este legat de

AGENȚIA FEDERALĂ DE EDUCAȚIE

INSTITUȚIA DE ÎNVĂȚĂMÂNT DE STAT DE ÎNVĂȚĂMUL PROFESIONAL SUPERIOR „UNIVERSITATEA AEROSPAȚIALĂ DE STAT SAMARA numită după Academicianul S.P. KOROLEV”

Iu. Zabolotnov

CONTROL OPTIM AL SISTEMELOR DINAMICE CONTINUE

Aprobat de Consiliul Editorial și Editurii al Universității ca suport didactic

SAMARA 2005

UDC 519.9+534.1

Recenzători: S.A. Ișkov, L.V. Kudiurov

Zabolotnov Yu.

Controlul optim al sistemelor dinamice continue: manual. indemnizatie / Iu. Zabolotnov; Samar. stat aerospațială univ. Samara, 2005. 149 p. : bolnav.

Manualul include o descriere a metodelor de control optim al sistemelor dinamice. O atenție deosebită este acordată soluționării optime a problemei de stabilizare pentru sistemele dinamice liniare. Odată cu prezentarea metodelor clasice de control optim al sistemelor liniare, bazate în principal pe principiul Bellman al programării dinamice, se are în vedere controlul aproximativ optim al sistemelor dinamice oscilatorii folosind metoda medierii.

Materialul manualului este inclus în cursul prelegerilor „Base teoretice ale controlului automatizat”, susținute de autor pentru studenții specialității 230102 - sisteme automate de prelucrare și control a informațiilor la catedrele de sisteme și tehnologii informaționale, matematică și mecanică ale SSAU . Cu toate acestea, manualul poate fi util pentru studenții altor specialități atunci când studiază teoria controlului optim al sistemelor dinamice.

PREFAŢĂ……………………………………………………. 5

1. PREVEDERI TEORETICE DE BAZĂ ALE CONTROLULUI OPTIM AL SISTEMELOR DINAMICE………………………………………………………………….. 8

1.1. Enunțarea problemei controlului optim al sistemelor dinamice…………………………………....8

1.2. Control optim software și problemă

stabilizare………………………………………………………. unsprezece

1.3. Mișcările neperturbate și perturbate ale unui sistem dinamic…………………………………………………….………….. 12

1.4. Enunțarea problemei stabilizării optime a mișcării pentru un sistem dinamic liniar……………..… 14

2. CONTROLABILITATE ȘI OBSERVABILITATE

SISTEME DINAMICE…………………………………………….….16

2.1. Transformări similare ale sistemelor dinamice liniare.16

2.2. Controlabilitatea sistemelor dinamice……………………….18

2.3. Observabilitatea sistemelor dinamice…………….21

3. PRINCIPIUL PROGRAMĂRII DINAMICE AL LUI BELLMAN ȘI TEORIA STABILITĂȚII LUI LIAPUNOV…….24

3.1. Principiul Bellman al programării dinamice…….24

3.2. Controlul optim al sistemelor dinamice liniare……………………………………………………..………… 29

3.3. Teoria stabilității a lui Lyapunov………………31

3.4. Conectarea metodei de programare dinamică cu teoria stabilității a lui Lyapunov …………………………………………... 37

4. DETERMINAREA CONTROLULUI OPTIM PENTRU SISTEME DINAMICE LINEARE…………… 39

4.1. Rezolvarea ecuației Bellman pentru sisteme dinamice liniare staționare..…………………………………………………………………………… 39

4.2. Rezolvarea ecuației Bellman pentru sisteme dinamice liniare nestaționare..…………………………………………………… 41

4.3. Despre alegerea criteriului de optimitate la rezolvarea problemei de stabilizare………………………………………………………………….43

4.4. Un exemplu de alegere optimă a coeficienților controlerului

la controlul unui sistem liniar de ordinul doi....……….. 47

5. SISTEME VIBRAȚIONALE DINAMICE ………….56

5.1. Mici oscilații ale sistemelor dinamice………….…56

5.2. Controlabilitatea și observabilitatea sistemelor dinamice liniare oscilatorii……………………………………………………………………………. 65

5.3. Metoda parametrilor mici……………………………………………….. 68

5.4. Metoda de mediere…………………………………………….… 72

5.5. Metoda de mediere pentru un sistem cu un grad de libertate... 76

5.6. Metoda de mediere pentru sisteme cu mai multe rapide

faze…………………………………………………………………………………. 79

5.7. Metoda de mediere pentru un sistem cu două puteri

libertatea………………………………………………………..…… 86

6. CONTROLUL OPTIM APROXIMATIV AL SISTEMELOR VIBRAȚIONALE DINAMICE.... 93

6.1. Controlul unui sistem oscilator liniar cu un grad de libertate…………………………………………………………………….… 93

6.2. Controlul unui sistem oscilator liniar cu două grade de libertate..………………………………………………………………………………. 106

6.3. Influența perturbațiilor neliniare asupra soluționării problemei de control optim……………//……………………………………… 115

LISTA SURSELOR UTILIZATE…..…………127

ANEXA 1. Transformări similare ale sistemelor dinamice liniare …………………………………………..…129

ANEXA 2. Studiu calitativ al sistemelor dinamice liniare pe planul de fază …………………… 134

ANEXA 3. Diferențierea funcțiilor cu un argument vectorial………………………………………………………... 142

ANEXA 4. Concepte de bază ale teoriei seriilor asimptotice……………………………………………………………………………. 143

ANEXA 5. Media trigonometrică

funcții…………………………………………………………….. 148

PREFAŢĂ

În mod tradițional, teoria clasică a controlului ia în considerare două probleme principale: problema determinării mișcării programului unui sistem dinamic și problema proiectării controlerelor care implementează un program dat de mișcare a obiectului de control (problema de stabilizare). Accentul principal al manualului este rezolvarea problemei de stabilizare, care este de obicei rezolvată folosind modele dinamice liniare. Fata de sistemele statice, in sistemele dinamice procesul se dezvolta in timp iar controlul in cazul general este si o functie a timpului.

La rezolvarea problemei de stabilizare se pot folosi diverse metode. Aici, în primul rând, trebuie remarcate metodele clasice ale teoriei controlului automat, bazate pe aparatul de funcții de transfer și caracteristici de frecvență. Cu toate acestea, apariția computerelor de mare viteză a condus la dezvoltarea de noi metode care stau la baza teoriei moderne de control. În teoria modernă a controlului, comportamentul unui sistem este descris în spațiul stărilor, iar controlul sistemului se reduce la determinarea acțiunilor optime, într-un anumit sens, de control asupra sistemului în fiecare moment în timp. Mai mult, modelele matematice ale sistemelor dinamice continue sunt de obicei sisteme de ecuații diferențiale obișnuite, în care timpul este variabila independentă.

La rezolvarea unei probleme de stabilizare, optimitatea controlului se intelege in sensul minimului unui anumit criteriu de optimitate (functional), care se scrie sub forma unei integrale definite. Criteriul de optimitate poate caracteriza diverse aspecte ale calității controlului: costuri de control (energie, combustibil etc.), erori de control (pentru diverse variabile de stare), etc. Pentru a determina controlul optim la rezolvarea problemei de stabilizare, se utilizează principiul clasic Bellman al programării dinamice.

Prima secțiune a manualului este introductivă: conține o formulare matematică a problemelor rezolvate în controlul sistemelor dinamice continue. A doua secțiune este dedicată problemelor care preced construirea controlului optim pentru sistemele liniare: probleme de controlabilitate și observabilitate. În a treia secțiune sunt derivate relațiile de bază ale principiului de programare dinamică Bellman, din care se determină în continuare controlul optim pentru un sistem dinamic liniar la rezolvarea problemei de stabilizare. În aceeași secțiune se arată că principiul Bellman al programării dinamice pentru sisteme liniare este legat organic de cea de-a doua metodă Lyapunov, a cărei îndeplinire a teoremelor oferă o soluție la problema de stabilizare. A patra secțiune a manualului prezintă algoritmi pentru determinarea controlului optim la rezolvarea problemei de stabilizare pentru un anumit criteriu de optimitate pătratică (integrandul funcționalului este o formă pătratică a variabilelor de control și stare ale sistemului). Este dat un exemplu de determinare a controlului optim cu un criteriu de optimitate dat pentru un sistem liniar specific. Secțiunea a cincea conturează bazele teoriei sistemelor oscilatorii dinamice. Sunt derivate relațiile de bază ale principiului de mediere, ceea ce face posibilă în multe cazuri simplificarea semnificativă a analizei și sintezei sistemelor oscilatorii. Secțiunea a șasea discută o metodă pentru determinarea unui control aproximativ optim pentru problema stabilizării prin sisteme oscilatorii. Sunt date exemple de control al sistemelor oscilatoare cu unul și două grade de libertate. Sunt analizate problemele posibilei influențe a perturbațiilor neliniare asupra rezolvării problemelor de stabilizare a sistemelor oscilatorii.

Metodele prezentate în manual fac posibilă găsirea unui control optim pentru rezolvarea problemelor de stabilizare a sistemelor dinamice sub formă de funcții analitice în funcție de variabilele de stare ale sistemului. În acest caz, ei spun că se rezolvă problema sintezei controlului. Aceste metode pot fi atribuite teoriei proiectării analitice a regulatorilor, care este una dintre direcțiile importante în dezvoltarea teoriei moderne de control.

Materialul din manual se bazează pe lucrări din domeniul teoriei controlului, care de-a lungul timpului au devenit deja clasice. Aici, în primul rând, este necesar să remarcăm lucrările lui L.S. Pontryagin. , Letova A.M. , Demidovich B.P. , Gropa D., Bellmana R., Moiseeva N.N., Bogolyubov N.N., Mitropolsky Yu.A. și alți oameni de știință renumiți interni și străini.

1. PUNCTE TEORETICE DE BAZĂ ALE CONTROLULUI OPTIM AL SISTEMELOR DINAMICE

1.1. Enunțarea problemei controlului optim al sistemelor dinamice

Modelele matematice ale sistemelor dinamice pot fi construite sub diferite forme. Acestea pot fi sisteme de ecuații diferențiale obișnuite, ecuații diferențiale parțiale, modele discrete corespunzătoare etc. O trăsătură distinctivă a descrierii matematice a oricărui sistem dinamic este că comportamentul său se dezvoltă în timp și este caracterizat de funcții ,..., care se numesc sisteme de variabile de stare (coordonate de fază). În cele ce urmează vom lua în considerare sistemele cu timp continuu. Mișcarea unui sistem dinamic poate fi controlată sau necontrolată. La implementarea mișcării controlate, comportamentul unui sistem dinamic depinde și de funcțiile de control,…. Să presupunem, de asemenea, că comportamentul sistemului este determinat în mod unic dacă sunt date funcția de control vectorial și starea inițială a fazei, unde este timpul inițial.

Ca model matematic al unui sistem dinamic, vom lua în considerare un sistem de ecuații diferențiale obișnuite scrise în formă normală Cauchy

unde , , este o funcție vectorială cunoscută.

Diverse modele matematice ale sistemelor dinamice cu timp continuu sunt cel mai adesea reduse la sistem (1.1). Deci, de exemplu, dacă comportamentul unui sistem dinamic este descris de un sistem de ecuații cu diferențe parțiale și are loc în spațiu și timp (modele matematice ale mecanicii continuumului), atunci, prin discretizare în spațiu (abordare cu elemente finite), ajungem la un sistem de ecuații diferențiale obișnuite similar cu (1.1), a cărui soluție este căutată în funcție de timp.

Ipoteza introdusă anterior despre unicitatea procesului de control pentru sistemul (1.1) este determinată de îndeplinirea condițiilor teoremei privind existența și unicitatea soluțiilor sistemelor de ecuații diferențiale obișnuite în formă Cauchy.

Să formulăm problema controlului optim al sistemului (1.1). În momentul inițial, sistemul (1.1) este în stare, este necesar să se determine un astfel de control care să transfere sistemul într-o stare finală dată (diferită de cea inițială), unde este timpul final. De obicei, se cere ca tranziția de la punct la punct (procesul de tranziție) să fie într-un anumit sens cea mai bună dintre toate tranzițiile posibile. De exemplu, dacă se ia în considerare un anumit sistem tehnic, atunci procesul de tranziție trebuie să satisfacă condiția energiei minime consumate sau condiția timpului minim de tranziție. Un astfel de cel mai bun proces de tranziție este de obicei numit procesul optim.

O funcție de control aparține de obicei unui domeniu de control, care este un set de spațiu euclidian -dimensional. În aplicațiile tehnice, se presupune că o regiune este o regiune închisă, adică o regiune care include limitele sale. Să numim control admisibil orice control care transferă sistemul de la un punct la altul. Pentru o comparație cantitativă a diferitelor controale admisibile se introduce un criteriu de optimitate, care, de regulă, este prezentat sub forma unor

Funcționala se calculează pe soluții ale sistemului (1.1) care îndeplinesc condițiile și , pentru un control admisibil dat .

În final, problema de control optim se formulează astfel: două puncte și sunt date în spațiul fazelor; dintre toate comenzile admisibile care transferă punctul de fază din poziție în poziție, găsiți unul pentru care funcțional (1.2) ia cea mai mică valoare.

Controlul care dă o soluție problemei prezentate mai sus se numește control optim și se notează cu , iar traiectoria corespunzătoare este traiectoria optimă.

Cometariu. Dacă este necesar să se asigure maximul unui criteriu, atunci această problemă poate fi redusă la problema găsirii minimului prin schimbarea formală a semnului în fața funcționalului (1.2).

Un caz special al problemei de control optim declarată este cazul când . Atunci functionala (1.2) ia forma iar optimitatea consta in implementarea timpului minim de tranzitie de la punct la punct. Această problemă de control optim se numește o problemă de performanță.

1.2. Software-ul de control optim și problemă de stabilizare

Să considerăm mișcarea sistemului dinamic (1.1). Să se găsească controlul optim pentru acest sistem și să se obțină traiectoria optimă corespunzătoare. La implementarea unei traiectorii optime în probleme tehnice, se întâmpină inevitabil dificultăți semnificative, care constau în imposibilitatea, în primul rând, de a seta cu precizie sistemul real (sau obiectul de control) la starea inițială, în al doilea rând, de a implementa cu acuratețe controlul optim în sine, și în al treilea rând, de a prezice cu acuratețe în prealabil condițiile externe de funcționare a sistemului (proximitatea modelului matematic original). Toate acestea conduc la necesitatea rezolvării problemei corectării legii optime de control în timpul funcționării oricărui sistem (sau obiect) tehnic. Astfel, problema controlului optim în condiții reale poate fi împărțită în două părți: 1) construirea unui control optim nominal al sistemului dinamic original în condiții ideale în cadrul modelului matematic (1.1); 2) construirea acțiunilor de control corectiv în vederea implementării unui control nominal optim dat și a unei traiectorii optime în timpul funcționării sistemului. Prima parte a problemei de control optim se numește de obicei problema construirii unui control optim al programului și este rezolvată în cadrul unor informații a priori cunoscute în prealabil despre sistemul luat în considerare. A doua parte a problemei se numește problema stabilizării unui program de control nominal dat și trebuie rezolvată în timpul funcționării sistemului folosind informațiile primite de la dispozitivele de măsurare ale sistemului de control. Problema stabilizării unui program de control nominal poate fi pusă și ca o problemă de găsire a controlului optim conform criteriului corespunzător, care se va face mai jos (vezi Secțiunea 1.4).

Cometariu. Evident, nu doar controlul optim poate fi folosit ca program de control nominal, ci și orice alt control admisibil (dacă problema de optimizare a controlului programului nu este rezolvată). În cel mai simplu caz particular, de exemplu, poate fi pusă sarcina de a stabiliza o anumită poziție constantă a sistemului.

1.3. Mișcarea neperturbată și perturbată a unui sistem dinamic

Deoarece mișcarea reală a sistemului diferă în mod inevitabil de mișcarea programului nominal, acest fapt a condus la conceptul de mișcări neperturbate și perturbate de Lyapunov A.A. . Astfel, orice mișcare program a sistemului (1.1), indiferent dacă este optimă sau admisibilă, se numește mișcare neperturbată. Mai mult, această mișcare corespunde unei soluții particulare a sistemului (1.1). Mișcarea perturbată este evaluată prin anumite abateri de la mișcarea neperturbată. În consecință, mișcarea perturbată va fi descrisă de următoarele variabile

unde variabilele și caracterizează programul de control nominal, iar variabilele și sunt abateri de la programul nominal.

Înlocuind relațiile (1.3) în sistemul (1.1), obținem

Adunând și scăzând același termen din partea dreaptă a sistemului (1.4) și ținând cont de faptul că

obţinem sistemul în abateri de la mişcarea nominală

unde , , și sunt determinate ca rezultat al rezolvării sistemului (1.5).

De obicei se consideră că abaterile de la mișcarea nominală sunt mici. Prin urmare, dacă extindem funcția într-o serie Taylor și introducem notația , , unde indicele (o) înseamnă că derivatele parțiale sunt determinate pentru un program nominal dat, obținem

Aici funcția determină termenii de ordinul doi și mai mari în abateri; matrice și selectați partea liniară a seriei și au componente și ; .

Ecuațiile scrise în abaterile (1.7) sunt de mare importanță în teoria controlului. Pe baza acestor ecuații se formulează un număr mare de probleme de optimizare de interes practic. Una dintre aceste probleme este problema de stabilizare formulată mai sus. Atunci când se rezolvă această problemă, este necesar să se determine cum trebuie selectate acțiunile corective de control pentru a reduce abaterile într-un anumit sens în cel mai bun mod.

1.4. Enunțarea problemei stabilizării optime a mișcării pentru un sistem dinamic liniar

Cel mai adesea, la rezolvarea problemei de stabilizare a mișcării unui sistem sau obiect de control, se folosește un sistem dinamic liniar în abateri, obținut din sistemul (1.7) prin eliminarea termenilor neliniari. Apoi

unde matricele și în cazul general sunt funcții de timp, deoarece depind de programul de control nominal. , iar apoi spun că problema sintezei controlului se rezolvă. După înlocuirea legii. Să luăm în considerare cazul în care matricea nu are mai multe valori proprii (identice). În acest caz, o astfel de transformare conduce matricea la o formă diagonală, unde este o matrice diagonală, pe a cărei diagonală principală se află valorile proprii ale matricei (dovada este dată în Anexa 1).

Introducere. Economia de piață din Ucraina necesită noi abordări ale managementului: criteriile economice și ale eficienței pieței vin în prim-plan. Progresul științific și tehnologic și dinamica mediului extern obligă întreprinderile moderne de producție să se transforme în sisteme mai complexe care necesită noi metode de management. Consolidarea orientării către piață a întreprinderilor și schimbările bruște ale mediului extern necesită dezvoltarea unor sisteme de management competitive menite să dezvolte decizii complexe de management și, prin urmare, abordări și algoritmi mai eficienți pentru rezolvarea problemelor la scară largă.

Lucrarea a fost efectuată în conformitate cu programul științific și tehnic de stat 6.22 - tehnologii informaționale avansate și planuri de sisteme pentru activități științifice și științifice-tehnice ale Ordinului Odesa al Institutului Lenin al Forțelor Terestre pentru anul 2004, conform temelor lucrărilor de cercetare .

Analiza cercetărilor recente În prezent, una dintre principalele și cele mai eficiente abordări pentru rezolvarea problemelor de control dimensional înalt este descompunerea. Această abordare combină un grup de metode bazate pe descompunerea problemei inițiale de înaltă dimensiune în subprobleme, fiecare dintre acestea fiind semnificativ mai simplă decât cea originală și poate fi rezolvată independent de celelalte. Conexiunea dintre subsarcinile individuale se realizează folosind o sarcină de „coordonare”, care este, de asemenea, mai simplă decât cea inițială. Pentru a face acest lucru, problema controlului este adusă într-o formă care satisface cerințele de descompunere, dintre care principalele sunt: ​​aditivitatea (separabilitatea) funcției obiectiv; natura de blocare a restricțiilor; prezența conexiunilor de bloc. Cu toate acestea, atunci când se rezolvă probleme practice de sinteză a controlului optim dimensional înalt, este adesea dificil să se satisfacă cerințele enumerate. De exemplu, calitatea funcționării unui sistem de producție poate fi evaluată printr-un criteriu de tip foarte general, care poate fi inseparabil în raport cu sarcinile de gestionare a subsistemelor individuale. Prin urmare, atunci când se convertește problema de control inițială într-o formă care satisface cerințele de descompunere, sunt inevitabile diverse simplificări, aproximări și diverse opțiuni pentru împărțirea problemei în subsarcini locale, de exemplu. blocuri de restricții și conexiuni între blocuri. Toți acești factori influențează atât calitatea soluției, cât și complexitatea calculelor la găsirea soluției optime.

Datorită absenței până în prezent a unor metode de evaluare calitativă a influenței factorilor enumerați asupra calității soluției, pare relevantă elaborarea unei metode de rezolvare a unei probleme de dimensiuni mari care să lase o anumită libertate în alegerea structurii locale. probleme, precum și satisfacerea și evaluarea impactului diverselor simplificări asupra calității soluțiilor.

Din analiza surselor din literatură rezultă că metodele numerice acceptabile pentru rezolvarea problemelor de optimizare neliniară sunt asociate cu costuri semnificative ale timpului și memoriei calculatorului, iar utilizarea liniarizării duce la pierderi în calitatea controlului. Prin urmare, este recomandabil ca noua metodă în curs de dezvoltare pentru rezolvarea problemei să-și păstreze natura neliniară, iar controlul optim să fie determinat în cadrul unei structuri de calcul descentralizate.

Obiectul cercetării îl reprezintă algoritmii de rezolvare a problemelor de control de dimensiuni mari.

Obiectul cercetării este dezvoltarea unei abordări bazate pe ideea de echivalență sau cvasi-echivalență a problemei inițiale cu dimensiuni mari și a problemei de descompunere a blocurilor corespunzătoare.

Sarcina științifică este de a dezvolta algoritmi, a căror utilizare ar asigura un control optim în cadrul unei structuri descentralizate, fără a fi necesar un schimb iterativ de informații între nivelurile de control.

Scopul lucrării este de a dezvolta și completa elemente de teorie aplicată și instrumente orientate către probleme pentru optimizarea problemelor de control de dimensiuni mari.

Noutatea științifică constă în dezvoltarea unei abordări a sintezei algoritmilor de optimizare pentru probleme de control la scară largă în cadrul unei structuri de calcul descentralizate, în care nu este nevoie de organizarea unui proces iterativ între nivelurile de control.

Material de bază.Fie ca problema controlului optim al unui sistem dinamic continuu luat în considerare să fie determinată de ecuația diferențială

(1)

după criteriu

(2)

la

unde - n m – vector de control dimensional; - n – o funcție dimensională ale cărei componente sunt diferențiabile continuu în raport cu argumentele; - funcţie scalară convexă, diferenţiabilă; - timpii inițial și respectiv final precizați.

Pentru a reprezenta obiectul de control (1) sub forma unei serii de subsisteme care interacționează, extindem (1) într-o serie Taylor relativ la punctul de echilibru

Unde ,

sau

(3)

În expresia (3), A și B reprezintă părți bloc-diagonale ale matricelor și, respectiv, cu blocuri și .

și și sunt părțile nediagonale și, respectiv.

Prin introducerea unui vector de relație în așa fel încât i – această componentă este determinată de expresie

, (4)

putem scrie ecuațiai– subsistemele

unde - este vectorul de control dimensional; - - vector dimensional de stare; - n – vector dimensional de relație.

Metoda de descompunere propusă pentru sintetizarea controalelor optime este următoarea. Subsistemul componente

iar ținând cont de relația cu alte subsisteme, o vom numi izolat.

Compoziția i – х i = 1,2,…, P subsistemele sunt reprezentate de model

(5)

unde și sunt matrici diagonale bloc cu blocuri și respectiv.

Să formulăm criteriul

, (6)

unde este o matrice diagonală bloc semidefinită pozitivă

cu blocuri; - matrice bloc-diagonală pozitiv-definită

cu blocuri - control optim.

Determinăm matrici și din condiția de cvasiechivalență a problemelor (1) – (2) și (5) – (6), care are forma

Aici , ,

Unde .

Pentru a determina elementele matriceale, avem un sistem de ecuații algebrice

. (7)

După rezolvarea ecuației (7), avem P probleme de optimizare independente în legătură cu structura bloc-diagonală a matricelor

,

Controlul optim local are forma

, (8)

, satisface ecuația diferențială liniară.

, . (9)

Soluția globală este o compoziție de soluții optime

. (10)

Concluzii. Astfel, problema sintetizării controlului optim pentru problema originală de înaltă dimensiune (1) – (2) se rezumă la următoarele: formularea problemelor de optimizare locală (5) – (6); determinarea parametrilor problemelor locale folosind formulele (3) și (6); rezolvarea problemelor locale conform (8) – (9); compoziţia soluţiilor locale (10).

Pierderile de calitate cu o abordare optimă a sintezei controalelor aproximativ optime pot fi estimate folosind formulele propuse în.

Noua abordare a rezolvării problemelor de control, bazată pe ideea de echivalență, este oferită o problemă inițială de mare dimensiune și conformă unitară offcompozită a unei probleme.

1. Mesarovic M., Mako D., Takahara I. Teoria sistemelor ierarhice pe mai multe niveluri. – M.: Mir, 1973.

2. Aesdon L.S. Optimizarea sistemelor mari. – M.: Mir, 1975.

3. Albrecht E.G. Despre stabilizarea optimă a sistemelor neliniare. – Matematică și mecanică aplicată, 1961, vol. 25.

4. Jivoglyadov V.P., Krivenko V.A. O metodă pentru descompunerea problemelor de control de dimensiuni mari cu un criteriu de calitate neseparabil. Rezumate ale celei de-a II-a Conferințe Interuniversitare Unisionale „Suport matematic, algoritmic și tehnic al sistemelor automate de control al proceselor”. Tașkent, 1980.

5. Hassan Mohamed, Sinqh Madan G. Optimizarea pentru sisteme neliniare folosind o nouă metodă pe două niveluri.„Automatica”, 1976, 12, Nr. 4.

6. Mahmoud M.S. Optimizare dinamică pe mai multe niveluri pentru o clasă de sisteme neliniare, „Int. J. Control”, 1979, 30, Nr. 6.

7. Krivenko V.A. Transformarea cvasi-echivalentă a modelelor de optimizare în probleme de sinteză a algoritmilor de control. – În carte: Adaptare și optimizare în sisteme mari. – Frunze, 1985.

8. Krivenko V.A. O metodă de sinteză a algoritmilor de control folosind ideea de modificare a funcției obiectiv. – Frunze, 1985.

9. Rumyantsev V.V. Despre stabilizarea optimă a sistemelor controlate. – Matematică și mecanică aplicată, 1970, numărul. 3.

10. Ovezgeldyev A.O., Petrov E.T., Petrov K.E. Sinteza si identificarea modelelor de evaluare si optimizare multifactoriala. – K.: Naukova Dumka, 2002.

Răspunsuri la întrebări

Ieșire colecție:

CONTROLUL OBIECTELOR DINAMICE COMPLEXE CU STRUCTURA VARIABILĂ

Markin Vasily Evghenievici

Ph.D. tehnologie. Științe, profesor asociat, Universitatea de Stat din Moscova. adm. G.I. Nevelskogo, Vladivostok

Vorobiev Alexey Yurievich

Ph.D. tehnologie. Științe, profesor asociat FEFU, Vladivostok

O sarcină urgentă a teoriei moderne de control este crearea de algoritmi și sisteme de control extrem de eficienți pentru controlul obiectelor dinamice complexe. Clasa de obiecte dinamice complexe include obiecte precum roboți manipulatori, vehicule subacvatice, mașini pentru prelucrare complexă etc. Trăsăturile caracteristice ale unor astfel de obiecte sunt dimensiunea mare a modelului matematic, neliniaritățile de diferite tipuri în modelul matematic, multiplicitatea, precum precum și incertitudinea structurală și parametrică semnificativă manifestată în procesul de funcționare.

Cauzele incertitudinii parametrice pot fi atât proprietățile dinamice ale obiectului însuși (de exemplu, o modificare a configurației unui manipulator duce la o modificare multiplă a momentului redus de inerție), cât și acțiunea mediului. Din punct de vedere matematic, acest tip de incertitudine poate fi evaluat după cum urmează:

Unde P i - un parametru. În timpul funcționării, parametrii obiectului pot lua o valoare din intervalul dintre valorile minime și maxime.

Pentru a sintetiza algoritmi și sisteme de control pentru obiecte dinamice complexe în condiții de incertitudine, sunt utilizate diverse abordări: adaptiv, robust, rețea neuronală etc. În această lucrare, un algoritm de control cu ​​structură variabilă este utilizat ca bază. Sistemele cu structură variabilă (SPS) care funcționează folosind acest algoritm sunt cunoscute de destul de mult timp ca sisteme de relee cu control discontinuu. Controlul cu o structură variabilă este de obicei construit sub următoarea formă:

(2)

Unde - ecuația suprafeței de comutare (alunecare) în spațiul de stare R n, care conține coordonatele de fază ale obiectului X 1 ,…X n. În mod tradițional, sunt considerate sisteme de ordinul doi, caz în care spațiul de stare degenerează într-un plan de fază, iar suprafața de comutare într-o linie de comutare. Ecuația suprafeței de comutare (linie) poate fi liniară sau neliniară. În cel mai simplu caz, linia de comutare este o linie dreaptă. În acest caz, suprafața de comutare este specificată de un anumit vector de parametri C dimensiuni (n ​​x 1), unde n- ordinea sistemului. O trăsătură caracteristică a sistemelor cu structură variabilă (VSS) este prezența așa-numitului mod de alunecare. Modul de alunecare este un mod dinamic special al sistemului, în care mișcarea are loc de-a lungul suprafeței de comutare s= 0 construit în spațiul fazelor R n(Fig. 1).

Poza 1. Modul de alunecare în SPS

Condiția principală pentru existența unui mod de alunecare este definită după cum urmează:

În modul de alunecare, sistemul funcționează într-un mod de comutare care, teoretic, are loc cu o frecvență infinit de înaltă. Traiectoria sistemului este determinată teoretic doar de ecuația liniei de comutare, care nu depinde de parametrii sistemului (de exemplu, de o sarcină variabilă). Procesele tranzitorii în modul de alunecare sunt stabile și monotone. Pentru a asigura proprietăți dinamice acceptabile ale sistemului, este necesară reglarea inițială a parametrilor, pentru care se folosește în mod tradițional metoda minimax: vector parametru c este ales astfel încât, pentru orice set de condiții inițiale, condiția existenței unui mod de alunecare (3) să fie îndeplinită. Cu alte cuvinte, valorile coeficienților liniei de comutare sunt selectate ținând cont de valoarea maximă a parametrului în schimbare p i max(1). Acest lucru face posibilă asigurarea apariției unui mod de alunecare în orice condiții inițiale. În același timp, performanța sistemului (care este determinată și de valorile elementelor vectorului c) devine scăzută. Acesta este unul dintre principalele dezavantaje ale SPS tradiționale. Pentru a crește performanța, se utilizează adaptarea în funcție de parametrul modului de alunecare. Algoritmul adaptiv pentru ajustarea coeficientului liniei de comutare c are următoarea formă:

(4)

Unde k c este coeficientul de proporționalitate, m, m d sunt valorile curente și, respectiv, de referință ale parametrului de alunecare.

Această lucrare examinează controlul adaptiv al conducerii unui robot de manipulare. Schema bloc a sistemului de control automat este prezentată în Fig. 2.

Desen 2 . Schema bloc a gradului de mobilitate a sistemului de control al conducerii

Pentru a implementa principiul variabilității structurii, controlul releului este utilizat în funcționare:

La randul lui,

, (6)

Unde c- coeficientul planului de alunecare (de comutare).

Pentru simulare a fost folosit pachetul Simulink inclus în Matlab. Rezultatele simulării sub forma unei traiectorii de fază tridimensională a sistemului sunt prezentate în Fig. 3.

Figura 3. Traiectorii de fază și procesele în timp ale unui sistem de ordinul trei: 1 - fără adaptare, 2 - cu adaptare.

Simulările arată o îmbunătățire semnificativă a performanței atunci când se utilizează controlul adaptiv. În plus, există o îmbunătățire semnificativă a indicatorilor dinamici de calitate în comparație cu algoritmii tradiționali de control.

O altă direcție de cercetare este asigurarea unei mai mari robustețe a algoritmilor de control în raport cu parametrii obiectului și controlerului. Astfel, au fost dezvoltați algoritmi pentru controlul unui obiect dinamic complex de ordin înalt în condiții de incertitudine parametrică semnificativă. Pe baza algoritmilor propuși, au fost sintetizate sisteme de control adaptiv. Au fost efectuate experimente numerice care au demonstrat eficiența ridicată a soluțiilor propuse.

Bibliografie:

1. Dyda A.A., Markin V.E. Sisteme de control cu ​​structură variabilă cu suprafețe de comutare pereche și neliniar deformabile. // Probleme de management. - 2005, nr 1. P. 22-25.

2.Markin V.E. Control suboptim al vitezei obiectelor dinamice complexe în condiții de incertitudine. / Proceedings of the XIII Baikal International School-Seminar on Optimization Methods. T. 2 - Irkutsk, 2005. P. 177-181.

3.Teoria sistemelor cu structură variabilă. / Ed. S.V. Emelyanova - M.: Nauka, Redacția principală a literaturii fizice și matematice, 1970 - 592 p.

4. Utkin V.I. Moduri de alunecare în probleme de optimizare și control. - M: Nauka, Redacția principală de literatură fizică și matematică, 1981 - 368 p.

5.Dyda A.A. Proiectarea algoritmilor VSS adaptivi pentru comenzile robotului manipulator. Proc. Prima conferință de control din Asia. Tokyo, 27-30 iulie 1994. pp 1077-1080.